Esempi di codice Python
Alcune esercizi con Python spiegati.
Possiamo scrivere e verificare questi programmi su:
- FARE, ambiente del Politecnico di Torino.
- Online GDB, ricordandoci di selezionare Python 3 da menù in alto a destra.
Numeri primi
In questo esempio vogliamo calcolare e stampare dei numeri primi. Definizione: un numero è primo se è divisibile solo per 1 e per sé stesso.
Per verificare se un numero a è divisibile per un numero b, usiamo
l’operatore modulo (%) che calcola il resto della divisione di a per b.
Verifichiamo se b è divisore di a controllando se a % b == 0.
In generale, per un numero n se non si trova un divisore fra 2 e n - 1, allora n è primo.
Esistono algoritmi sicuramente più complessi e efficienti per verificare se un numero è primo ma noi useremo questo algoritmo semplice. I numeri primi sono fondamentali in matematica e informatica, in particolare per la crittografia: c’è tanto tanto lavoro universitario e di centri di ricerca ma a noi va bene così.
Separiamo allora l’esercizio in più parti.
Controllare se un numero è primo
Chiediamo all’utente un numero n e verifichiamo se è primo:
n = int(input("Inserisci un numero"))
# Il numero è primo fino a prova contraria
is_prime = True
# Cerchiamo quindi le prove contrarie, cerchiamo cioè
# se esiste almeno un divisore fra 2 e n - 1.
for d in range(2, n): # range(2, n) esclude n
if n % d == 0: # se d è divisore di n
is_prime = False # allora n non è primo
break # Non è necessario, ma leggi sotto
# Stampiamo il risultato
if is_prime:
print(n, "è primo")
else:
print(n, "non è primo")
Il cuore dell’algoritmo, il ciclo for, ricerca i potenziali divisori d
nell’intervallo fra 2 e n - 1, usando range(2, n) che include
nell’intervallo il 2 ma non include l’n.
L’istruzione break serve per abbreviare il calcolo. Avendo trovato
un divisore, non ha senso continuare a cercare quindi break blocca
il ciclo for prima che questo si concluda. Non è essenziale farlo.
Stampa dei numeri primi fino a 1000
Capito come si controlla se un numero è primo o meno, possiamo usare il cuore dell’esempio precedente per stampare tutti i numeri primi che si trovano fino a 1000. Non serve più chiedere all’utente niente.
for n in range(2, 1000 + 1): # andiamo a cercare i numero fino a 1000 incluso
is_prime = True
for d in range(2, n): # range(2, n) esclude n
if n % d == 0:
is_prime = False
break
if is_prime:
print(n)
Vediamo che il numero primo più grande prima di 1000 è 997.
Stampa dei primi 1000 numeri primi
Un’altra variante potrebbe essere quella di stampare tutti i numeri primi finché non se ne trovino 1000.
Usiamo un while e contiamo quanti ne troviamo.
Non possiamo usare un for perché non sappiamo questi
1000 numeri quali sono e quindi fino a che numero cercare.
found = 0 # qui contiamo quanti ne abbiamo trovati
n = 2 # partiamo da 2
# Andiamo alla ricerca fino a quando non ne troviamo 1000
while found < 1000:
# Verifichiamo n
is_prime = True
for d in range(2, n): # range(2, n) esclude n
if n % d == 0:
is_prime = False
break
# n è primo, segnamocelo
if is_prime:
found = found + 1
print(n)
# Prossimo n
n = n + 1
Ci mette un po’ perché troveremo che il millesimo numero primo è 7919. Più un numero è grande e più ci mette a fare il controllo.
Vedete quanto ci mette e poi provate a vedere quanto ci mette senza break.
Vedrete che ci impiegherà molto di più.
Tavola pitagorica
Vogliamo generare una tavola pitagorica 10x10, dove sono rappresentate tutte le tabelline da 1 a 10, cioè tutte le possibili moltiplicazioni fra i numeri da 1 a 10.
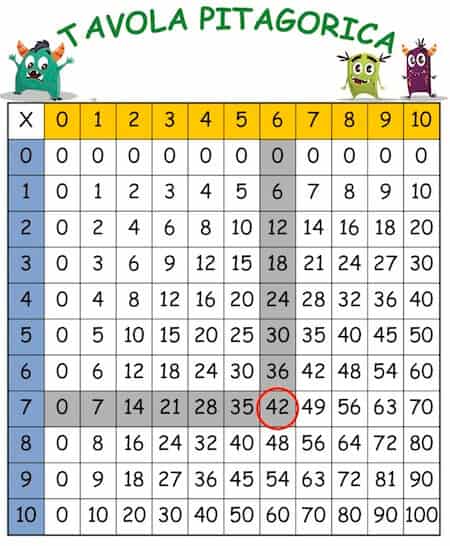
Non vogliamo una tabella con tutti i bordi e i colori, ma semplicemente i numeri a formare un quadrato, possibilmente incolonnati bene. Non vogliamo neanche le righe e le colonne con lo zero.
Per ogni numero x e y compreso fra 1 e 10, vogliamo stampare il loro prodotto.
La frase precedente può essere quasi trascritta in Python direttamente:
for x in range(1, 11): # fino a 10, cioè 11 escluso
for y in range(1, 11):
print(x * y)
Questo stampa un elenco di 100 numeri. Miglioriamo l’esercizio andando a capo correttamente, solo alla fine cioè di ogni riga:
for x in range(1, 11): # fino a 10, cioè 11 escluso
for y in range(1, 11):
print(x * y, end=" ") # non va a capo ma lascia uno spazio
print() # va a capo
Il parametro end=" " fa si che invece di terminare la stampa del numero
andando a capo, come normalmente avviene, si aggiunge uno spazio. Così facendo
i numeri non vengono più stampati in un’unico elenco, ma in un’unica riga.
Aggiungendo poi il secondo print() a fine di ogni riga, cioè alla fine
di ogni ciclo for esterno, questo va a capo.
Si forma una tabella 10x10 di numeri, sebbene non incolonnata benissimo in quanto i numeri minori di 10 occupano un solo carattere invece che 2 rendendo la tabella ammaccata.
Proviamo a risolverlo così:
for x in range(1, 11): # fino a 10, cioè 11 escluso
for y in range(1, 11):
n = x * y
if n < 10:
print("", end=" ") # stampa uno spazio e non va a capo
print(n, end=" ") # non va a capo ma lascia uno spazio
print() # va a capo
Che produce questo risultato:
1 2 3 4 5 6 7 8 9 10
2 4 6 8 10 12 14 16 18 20
3 6 9 12 15 18 21 24 27 30
4 8 12 16 20 24 28 32 36 40
5 10 15 20 25 30 35 40 45 50
6 12 18 24 30 36 42 48 54 60
7 14 21 28 35 42 49 56 63 70
8 16 24 32 40 48 56 64 72 80
9 18 27 36 45 54 63 72 81 90
10 20 30 40 50 60 70 80 90 100
Roulette
(da pubblicare)